Ejercicio 1
Polinomio de Bernstein y curvas de Bézier
Contents
- Apartado a: Función que calcula el factorial de un número
- Apartado b: Función que calcula las combinaciones de dos números
- Apartado c parte 1: Función que devuelve el valor del polinomio de Bernstein para un valor del parámetro t
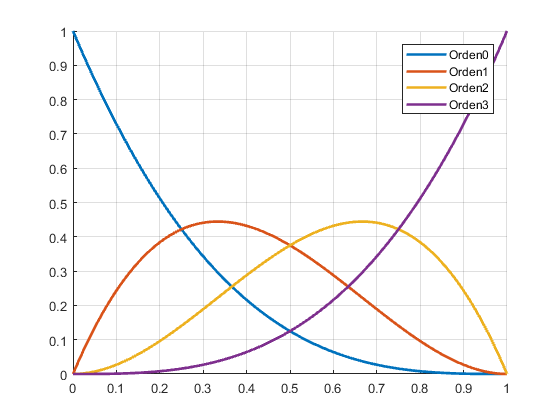
- Apartado c parte 2: Gráfica de los polinomios de Bernstein de grado 3
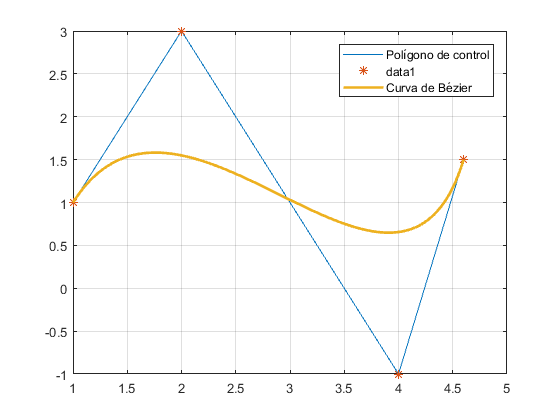
- Apartado d: Gráfica del polígono de control y curva de Bézier de los puntos Vi dados
Apartado a: Función que calcula el factorial de un número
La función factr(n) calcula el factorial de n
n es un número natural
function x=factr(n) if n<0; error('El número n ha de ser positivo'); end if n==0 || n==1 ; x=1; else x=n*factr(n-1); end;
Apartado b: Función que calcula las combinaciones de dos números
La función combina(n,i) calcula n sobre i
n e i son números naturales
function x=combina(n,i); x=factr(n)/(factr(i)*factr(n-i)); end
Apartado c parte 1: Función que devuelve el valor del polinomio de Bernstein para un valor del parámetro t
La funcion bernstein(t,n,i) calcula el valor del polinomio de Bernstein de grado n y orden i
function x=bernstein(t,n,i); x=combina(n,i)*t^i*(1-t)^(n-i); end;
Apartado c parte 2: Gráfica de los polinomios de Bernstein de grado 3
x=linspace(0,1,100); figure('Name','Polinomios de Bernstein de grado 3') hold on grid on n=3; for i=0:n; y=[]; for j=1:length(x); y=[y bernstein(x(j),3,i)]; end; name=strcat('Orden ',num2str(i)); plot(x,y,'LineWidth',2,'DisplayName',name); end; legend show
Apartado d: Gráfica del polígono de control y curva de Bézier de los puntos Vi dados
Vx=[1, 2, 4, 4.6]; Vy=[1, 3, -1, 1.5]; figure('Name','Curva de Bézier y polígono de control') plot(Vx,Vy,'DisplayName','Polígono de control') hold on grid on plot(Vx,Vy,'*') t=0:0.01:1; n=length(Vx)-1; Qx=[]; Qy=[]; for j=1:length(t); tempx=0; tempy=0; for i=0:n; tempx=tempx+Vx(i+1)*bernstein(t(j),n,i); tempy=tempy+Vy(i+1)*bernstein(t(j),n,i); end; Qx=[Qx tempx]; Qy=[Qy tempy]; end; plot(Qx,Qy,'LineWidth',2,'DisplayName','Curva de Bézier') legend show