Ejercicio 3
Resolución de un sistema masa-resorte-amortiguador utilizando ODE45
Contents
Sistema de EDOs de primer orden
Definición del sistema de ecuaciones diferenciales que describen elconjunto masa-resorte-amortiguador
function x=sistema(t,x,c) m=20; k=20; x=[x(2);(1/m)*(-k*x(1)-c*x(2))]; end
ODE45
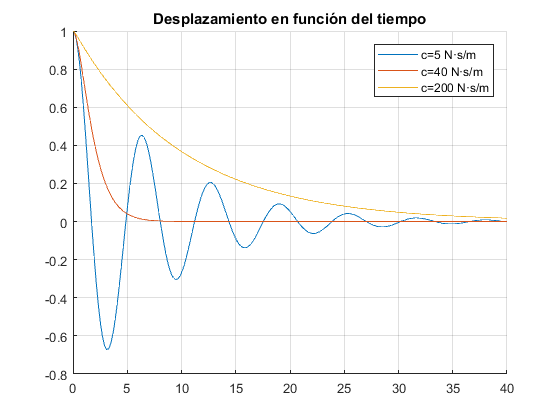
v0=0; x0=1; t0=0; tf=40; c=[5 40 200]; figure('Name','Posición-tiempo en sistema masa-resorte-amortiguador') hold on grid on for i=1:length(c) [t,x]=ode45(@sistema,[t0 tf],[x0 v0],[],c(i)); name=strcat('c=',num2str(c(i)),' N·s/m'); plot(t,x(:,1),'DisplayName',name) end legend show title('Desplazamiento en función del tiempo')